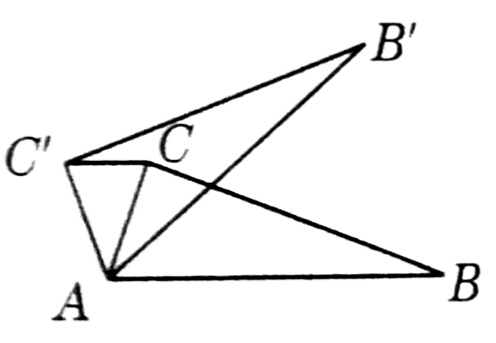
1、如图，在△ABC中，∠CAB=70°，在同一平面内，将△ABC绕点A旋转到△AB'C'的位置，使得CC'// AB，则∠BAB'的度数为_____。
A.30°           B.35°         C.40°              D.50°
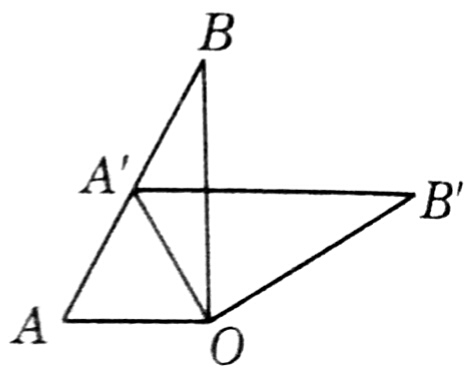
2、如图，∠AOB=90°，∠B=30°，△A'OB'可以看作是由△AOB绕点O顺时针旋转n°得到的，若点A'在AB上，则n的大小是______。
A.30          B.45               C.60              D.90
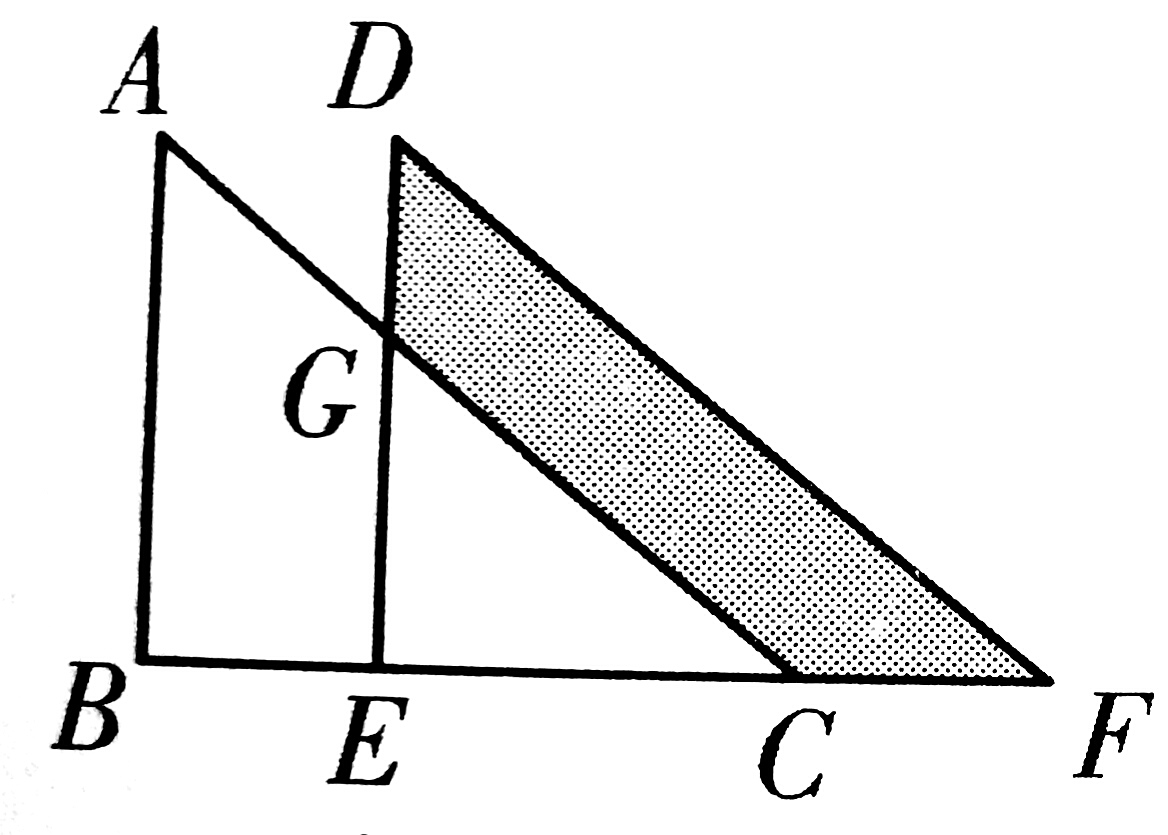
3、如图，将Rt△ABC沿BC边向右平移得到直角△DEF，AB=8，BE=6，DG=3，则阴影
部分的面积为_______。
A.30          B.35               C.39              D.42
                                            
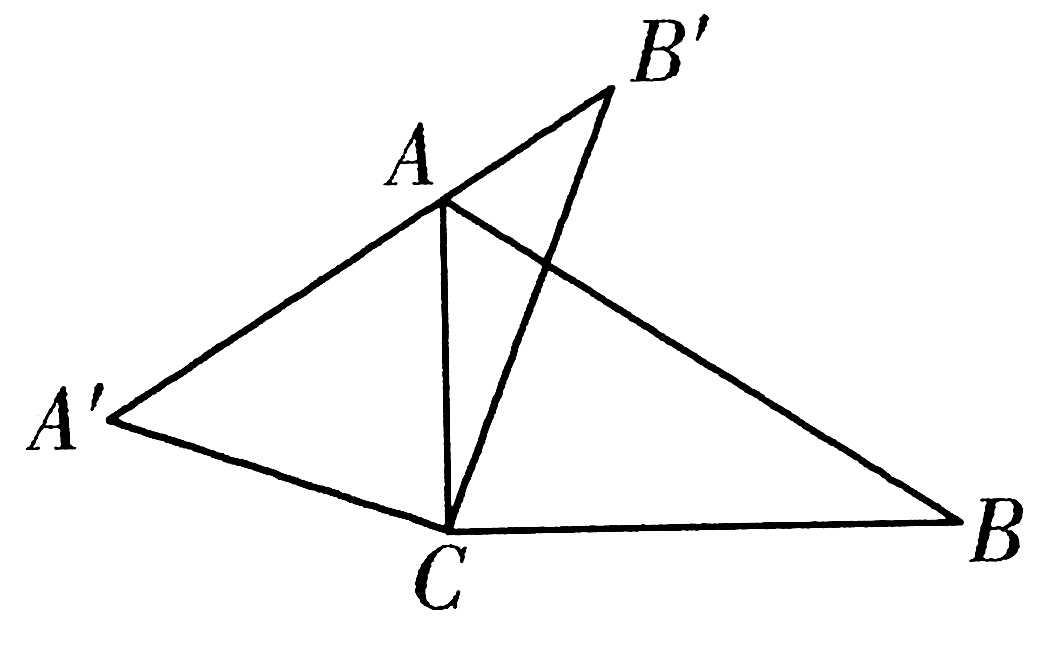
4、如图，△ABC 是直角三角形，∠ACB=90°，∠B=30°，以点C为旋转中心，将△ABC旋转到△A'B'C的位置，且使A'B'经过点A。
(1)求∠ACA'的度数，判断△ACA'的形状。
(2)求线段AC与线段AB的数量关系。
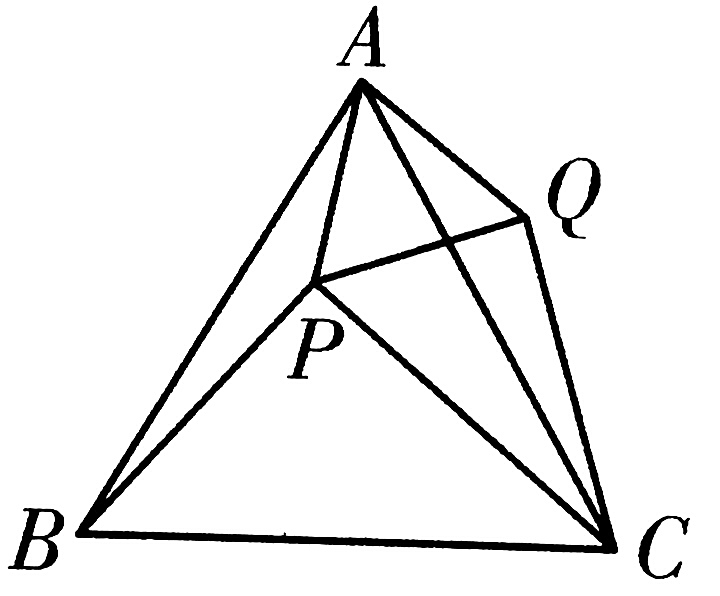
5、已知，点P是等边三角形△ABC中一点，线段AP绕点A逆时针旋转60°到AQ，连接PQ，QC。
(1)求证：PB=QC
(2)若PA=3，PB=4，∠APB=150°，求 PC的长度。
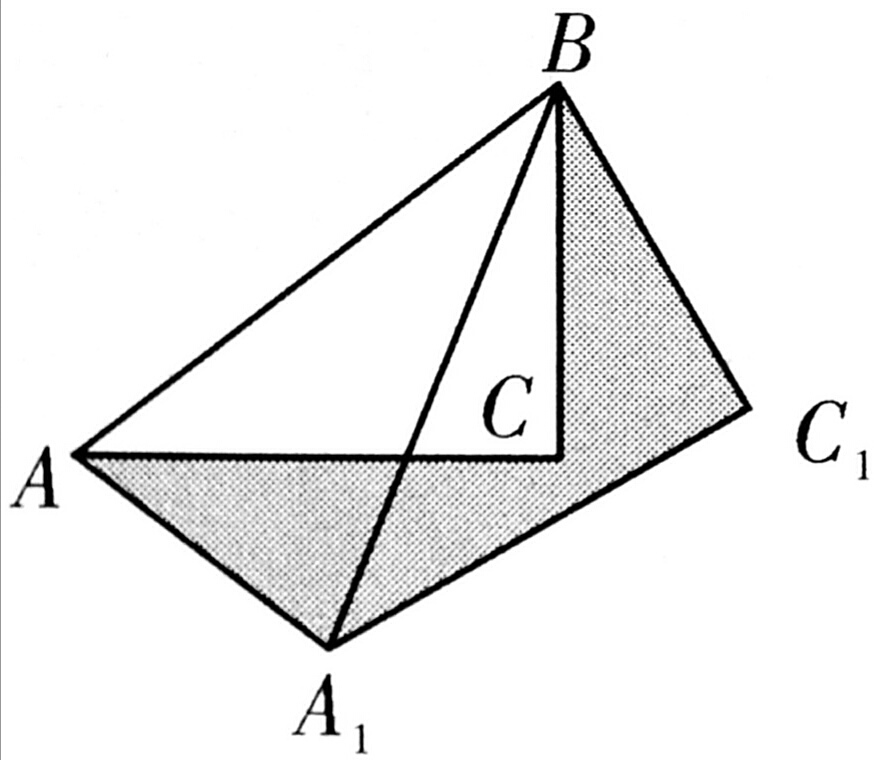
6、如图，在△ABC 中，AB=6，将△ABC绕点B按逆时针方向旋转30°后得到△A₁BC₁，求图中阴影部分的面积？
                                                
参考答案：1-3 CCC
4、(1)∵∠A'=60°(∠B'=∠B=30°)
                A'C=AC (对应边)
           ∴∠A'AC=60°
          ∴∠ACA'=60° (△A'AC中)
           ∴△ACA'是等边三角形(三个内角60度)
       (2)30°角所对边等于斜边一半
       ∴AC=1/2AB
           或AB=2AC
5、(1)∵∠BAC=60° (等边三角形)
              P旋转60°
         ∴∠BAP=∠CAQ
         在△ABP和△ACQ中
            AB=AC(等边三角形)
           ∠BAP=∠CAQ(已证)
            AP=AQ(旋转不变)
          ∴△ABP≌△ACQ
         ∴PB=QC(对应边相等)
    (2)由以上得知：△APQ是等边三角形
        ∴PQ(=PA)=3
          ∠PQC=∠AQC—∠AQP=150—60=90°
       而QC=PB(全等已证)
      在直角三角形△PQC中
            PC²=PQ²+QC²
        即PC²=3²+4²
          ∴PC=5
6、①∵∠ABA₁=30°(旋转30°)
         ∴AB边上的高=1/2·AB=3
         ∴S△ABA₁=6×3÷2=9
    ②S阴影=(S△ABA₁+S△A₁BC₁)—S△ABC
            而△ABC=△A₁BC₁
    ③∴S阴影=S△ABA₁
              即阴影部分面积是9

潜龙家教谭老师全程做题并录入，时间精力有限错漏之处恳请指正，谢谢！